Horizontal wells#
A horizontal well is located in a 20 m thick aquifer; the hydraulic conductivity is \(k = 10\) m/d and the vertical anisotropy factor is 0.1. The horizontal well is placed 5 m above the bottom of the aquifer. The well has a discharge of 10,000 m\(^3\)/d and radius of \(r=0.2\) m. The well is 200 m long and runs from \((x, y) = (−100, 0)\) to \((x, y) = (100, 0)\). A long straight river with a head of 40 m runs to the right of the horizontal well along the line \(x = 200\). The head is fixed to 42 m at \((x, y) = (−1000, 0)\).
Three-dimensional flow to the horizontal well is modeled by dividing the aquifer up in
11 layers; the elevations are: [20, 15, 10, 8, 6, 5.5, 5.2, 4.8, 4.4, 4, 2, 0]. At
the depth of the well, the layer thickness is equal to the diameter of the well, and it
increases in the layers above and below the well. A steady timflow model is created with the
Model3D command. The horizontal well is located in layer 6 and is modeled with the
Ditch element. Initially, the entry resistance of the well is set to zero.
import matplotlib.pyplot as plt
import numpy as np
import timflow.steady as tfs
figsize = (6, 6)
z = [20, 15, 10, 8, 6, 5.5, 5.2, 4.8, 4.4, 4, 2, 0]
ml = tfs.Model3D(kaq=10, z=z, kzoverkh=0.1)
ls1 = tfs.Ditch(ml, x1=-100, y1=0, x2=100, y2=0, Qls=10000, order=5, layers=6)
ls2 = tfs.RiverString(
ml,
[(200, -1000), (200, -200), (200, 0), (200, 200), (200, 1000)],
hls=40,
order=5,
layers=0,
)
rf = tfs.Constant(ml, xr=-1000, yr=0, hr=42, layer=0)
Questions:#
Exercise 4a#
Solve the model.
ml.solve()
Number of elements, Number of equations: 3 , 31
.
.
.
solution complete
Exercise 4b#
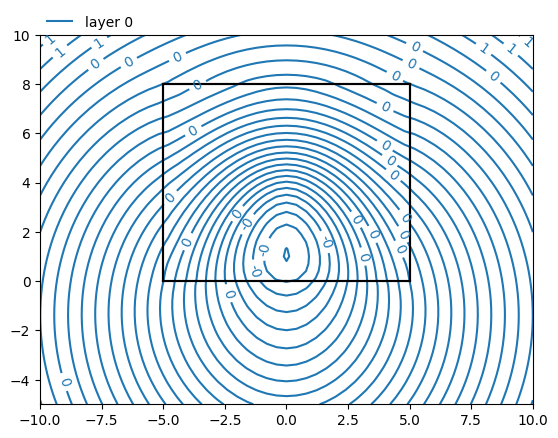
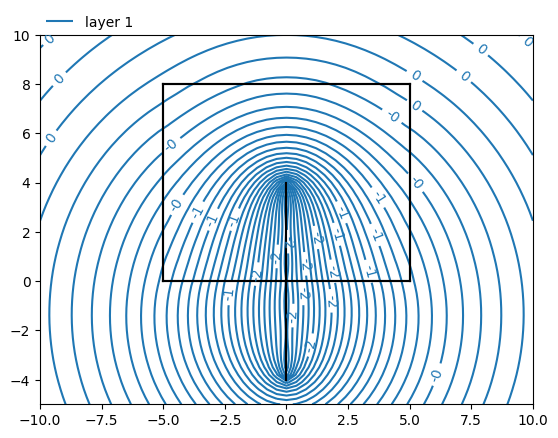
Create contour plots of layers 0 and 6 and note the difference between the layers. Also, compute the head at \((x, y) = (0, 0.2)\) (on the edge of the well) and notice that there is a very large head difference between the top of the aquifer and the well.
ml.plots.contour(
win=[-150, 150, -150, 150], ngr=[50, 100], layers=[0, 6], figsize=figsize
)
print("The head at the top and in layer 6 are:")
print(ml.head(0, 0.2, [0, 6]))
The head at the top and in layer 6 are:
[24.75850319 13.05654353]
Exercise 4c#
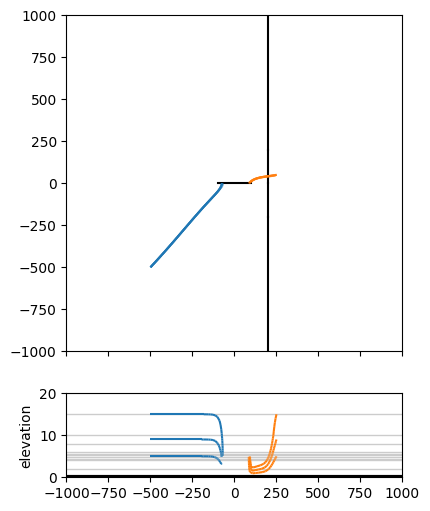
Draw a number of pathlines from different elevations using the tracelines command. First make a plot with a cross section below it.
axes = ml.plots.topview_and_xsection(win=[-1000, 1000, -1000, 1000], figsize=figsize)
ml.plots.tracelines(
xstart=[-500, -500, -500],
ystart=[-500, -500, -500],
zstart=[5, 9, 15],
hstepmax=20,
tmax=10 * 365.25,
orientation="both",
color="C0",
ax=axes,
)
ml.plots.tracelines(
xstart=[250, 250, 250],
ystart=[50, 50, 50],
zstart=[5, 9, 15],
hstepmax=20,
tmax=10 * 365.25,
orientation="both",
color="C1",
ax=axes,
)
.
.
.
.
.
.
array([<Axes: >, <Axes: ylabel='elevation'>], dtype=object)
Exercise 4d#
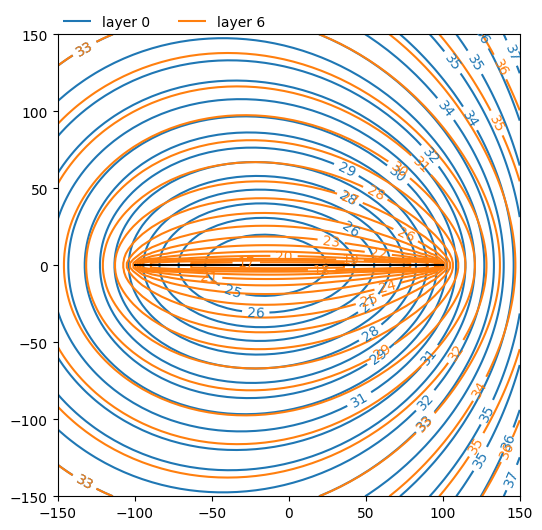
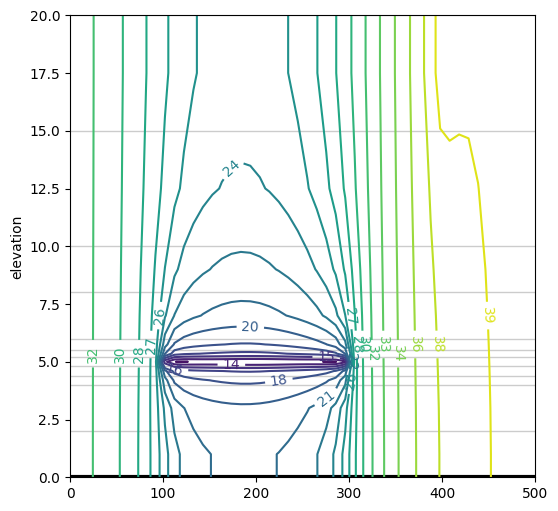
Make a contour plot of the heads in a vertical cross-section using the vcontour command. Use a cross-section along the well.
ml.plots.vcontour(win=[-200, 300, 0, 0], n=50, levels=20, figsize=figsize)
<matplotlib.contour.QuadContourSet at 0x716104f6ca50>
Exercise 4e#
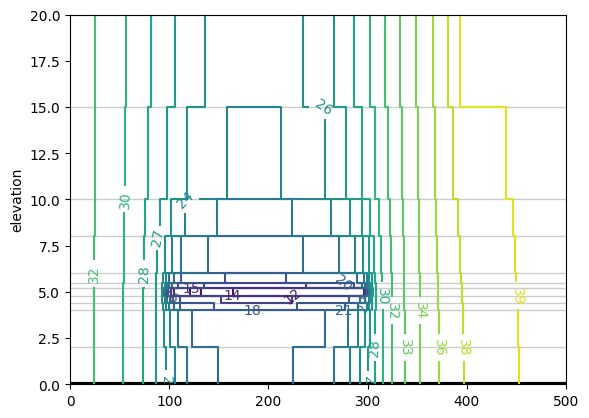
Change the entry resistance of the horizontal well to 0.01 days and set the width to 0.4 m and resolve the model. Notice the difference in the head inside the horizontal well with the headinside function of the horizontal well. Use a
print("head inside w/o resistance:")
print(ls1.headinside())
head inside w/o resistance:
[12.1087613]
ml = tfs.Model3D(kaq=10, z=z, kzoverkh=0.1)
ls = tfs.Ditch(
ml, x1=-100, y1=0, x2=100, y2=0, Qls=10000, order=5, layers=6, wh=0.4, res=0.01
)
tfs.RiverString(
ml,
[(200, -1000), (200, -200), (200, 0), (200, 200), (200, 1000)],
hls=40,
order=5,
layers=0,
)
rf = tfs.Constant(ml, xr=-1000, yr=0, hr=42, layer=0)
ml.solve()
Number of elements, Number of equations: 3 , 31
.
.
.
solution complete
print("head inside horizontal well:", ls.headinside())
head inside horizontal well: [10.83630693]
ml.plots.vcontour(win=[-200, 300, 0, 0], n=50, levels=20, vinterp=False)
<matplotlib.contour.QuadContourSet at 0x716102adec10>
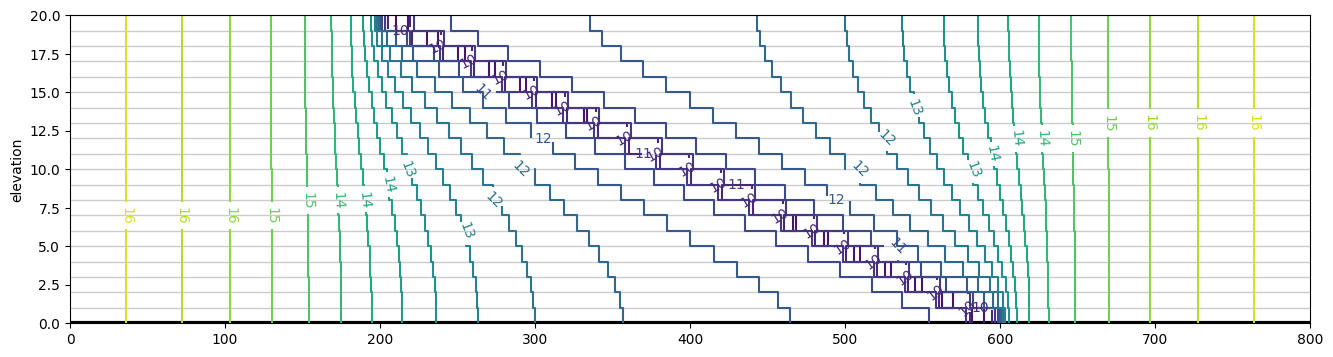
Slanted well#
A slanted well may be simulated by putting different sections in different layers
z = [20, 15, 10, 8, 6, 5.5, 5.2, 4.8, 4.4, 4, 2, 0]
ml = tfs.Model3D(kaq=10, z=np.linspace(20, 0, 21), kzoverkh=0.1)
rf = tfs.Constant(ml, 0, 1000, 20)
x = np.linspace(-200, 200, 21)
y = np.zeros(21)
ls = tfs.RiverString(
ml, xy=list(zip(x, y, strict=False)), hls=10, layers=np.arange(0, 20, 1), order=0
)
ml.solve()
Number of elements, Number of equations: 2 , 21
.
.
solution complete
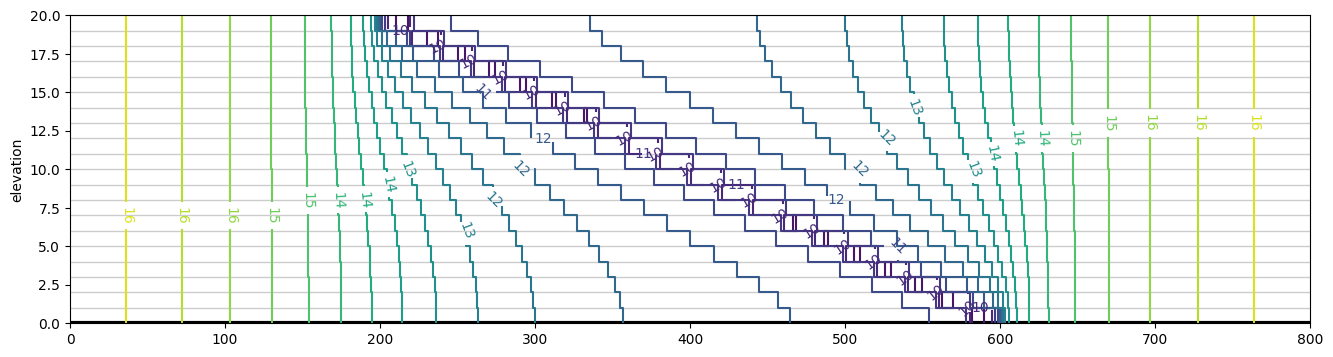
ml.plots.vcontour(win=[-400, 400, 0, 0], n=200, levels=20, vinterp=False, figsize=(16, 4))
<matplotlib.contour.QuadContourSet at 0x716105750410>
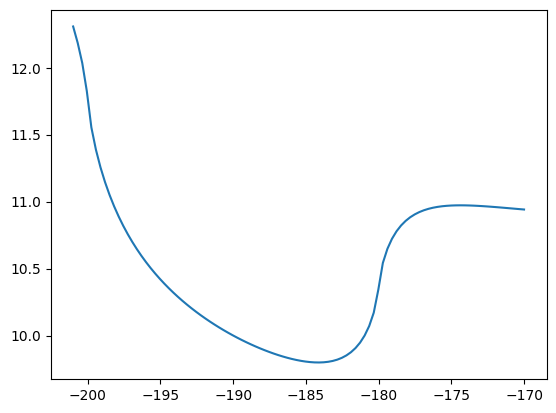
Note that the head is not exactly constant along the line-sink segments when using order 0
h = ml.headalongline(np.linspace(-201, -170, 100), 0)
plt.plot(np.linspace(-201, -170, 100), h[0])
[<matplotlib.lines.Line2D at 0x71610569a710>]
Qtot = np.sum(ls.discharge())
print("Discharge of slanted well when modeled with fixed head hls=10:", Qtot)
Discharge of slanted well when modeled with fixed head hls=10: 4193.946003637199
z = [20, 15, 10, 8, 6, 5.5, 5.2, 4.8, 4.4, 4, 2, 0]
ml = tfs.Model3D(kaq=10, z=np.linspace(20, 0, 21), kzoverkh=0.1)
rf = tfs.Constant(ml, 0, 1000, 20)
x = np.linspace(-200, 200, 21)
y = np.zeros(21)
ls = tfs.DitchString(
ml, xy=list(zip(x, y, strict=False)), Qls=Qtot, layers=np.arange(0, 20, 1), order=0
)
ml.solve()
Number of elements, Number of equations: 2 , 21
.
.
solution complete
ml.plots.vcontour(win=[-400, 400, 0, 0], n=200, levels=20, vinterp=False, figsize=(16, 4))
<matplotlib.contour.QuadContourSet at 0x716104aaa210>
print("Head in slanted well when modeled with fixed discharge:")
[print(lspart.headinside()) for lspart in ls.lslist];
Head in slanted well when modeled with fixed discharge:
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
[10.]
Lake with a horizontal well#
import timflow.steady as tfs
ml = tfs.ModelMaq(kaq=[1, 2], z=[10, 5, 4, 0], c=20)
xy = [(-5, 0), (0, 0), (5, 0), (5, 8), (-5, 8)]
p1 = tfs.PolygonInhomMaq(
ml,
xy=xy,
kaq=[0.2, 8],
z=[11, 10, 5, 4, 0],
c=[2, 20],
topboundary="semi",
hstar=1.0,
order=3,
ndeg=1,
)
w = tfs.Well(ml, xw=0, yw=-10, Qw=100, layers=1)
rf = tfs.Constant(ml, xr=0, yr=-100, hr=2)
ml.solve()
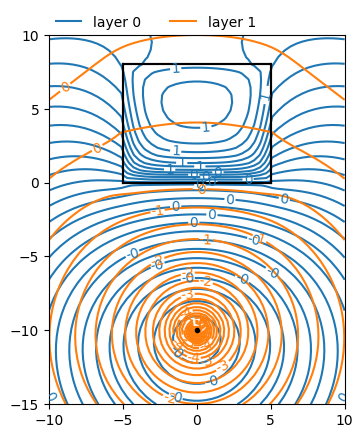
ml.plots.contour([-10, 10, -15, 10], 50, [0, 1], 30)
Number of elements, Number of equations: 13 , 81
.
.
.
.
.
.
.
.
.
.
.
.
.
solution complete
<Axes: >
ml = tfs.ModelMaq(kaq=[1, 2], z=[10, 5, 4, 0], c=20)
xy = [(-5, 0), (0, 0), (5, 0), (5, 8), (-5, 8)]
p1 = tfs.PolygonInhomMaq(
ml,
xy=xy,
kaq=[0.2, 8],
z=[11, 10, 5, 4, 0],
c=[2, 20],
topboundary="semi",
hstar=1.0,
order=5,
ndeg=2,
)
ls1 = tfs.DitchString(ml, [(0, -4), (0, 0), (0, 4)], 100, order=3, layers=[1])
rf = tfs.Constant(ml, xr=0, yr=-100, hr=2)
ml.solve()
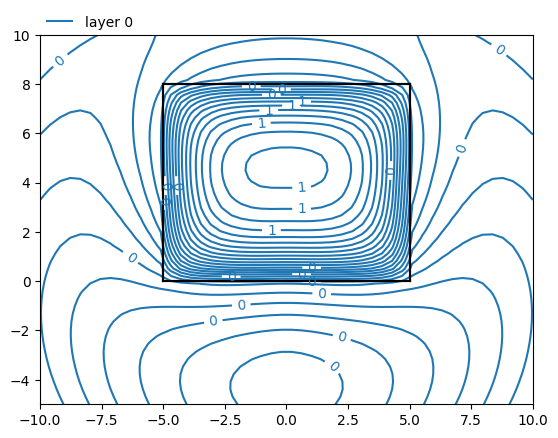
ml.plots.contour([-10, 10, -5, 10], 50, [0], 30)
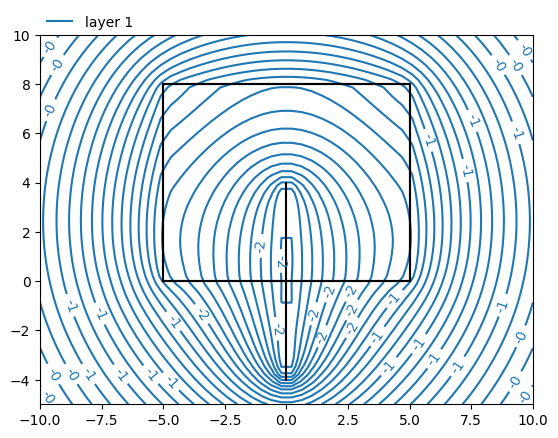
ml.plots.contour([-10, 10, -5, 10], 50, [1], 30)
Number of elements, Number of equations: 13 , 129
.
.
.
.
.
.
.
.
.
.
.
.
.
solution complete
<Axes: >
for ls in ls1.lslist:
for i in range(ls.ncp):
print(ml.head(ls.xc[i], ls.yc[i], ls.layers))
[-2.28658741]
[-2.28658741]
[-2.28658741]
[-2.28658741]
[-2.28658741]
[-2.28658741]
[-2.28658741]
[-2.28658741]
ml = tfs.ModelMaq(kaq=[1, 2], z=[10, 5, 4, 0], c=20)
xy = [(-5, 0), (0, 0), (5, 0), (5, 8), (-5, 8)]
p1 = tfs.PolygonInhomMaq(
ml,
xy=xy,
kaq=[1, 2],
z=[11, 10, 5, 4, 0],
c=[2, 2],
topboundary="semi",
hstar=1.0,
order=5,
ndeg=2,
)
ls1 = tfs.DitchString(ml, [(0, -4), (0, 0), (0, 4)], 100, order=3, layers=[1])
rf = tfs.Constant(ml, xr=0, yr=-100, hr=2)
ml.solve()
ml.plots.contour([-10, 10, -5, 10], 51, [0], 30)
ml.plots.contour([-10, 10, -5, 10], 51, [1], 30)
Number of elements, Number of equations: 13 , 129
.
.
.
.
.
.
.
.
.
.
.
.
.
solution complete
<Axes: >