Test polygon area sink

import matplotlib.pyplot as plt
import numpy as np

import timflow.steady as tfs

ml = tfs.ModelMaq(kaq=[1, 2], z=[10, 5, 4, 0], c=2)
xy = [(-50, 0), (50, 0), (50, 80), (-50, 80)]
p1 = tfs.PolygonInhomMaq(
    ml,
    xy=xy,
    kaq=[1, 2],
    z=[10, 5, 4, 0],
    c=[2],
    topboundary="conf",
    N=0.01,
    order=5,
    ndeg=3,
)
rf = tfs.Constant(ml, xr=0, yr=-1000, hr=2)
ml.solve()

Number of elements, Number of equations: 11 , 98
.
.
.
.
.
.
.
.
.
.
.

solution complete

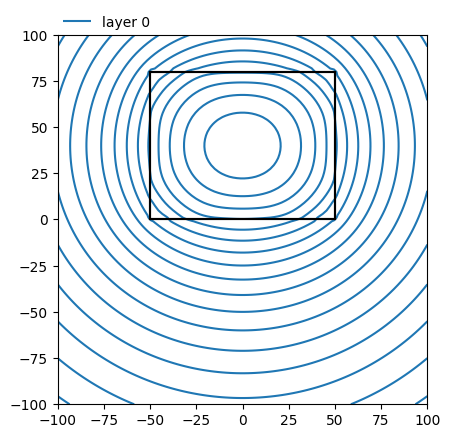
ml.plots.contour(win=[-100, 100, -100, 100], ngr=100, layers=[0], levels=20, labels=False)

<Axes: >

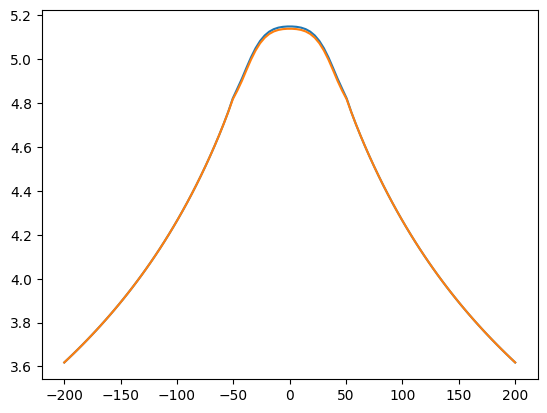
x = np.linspace(-200, 200, 100)
h = ml.headalongline(x, 3)
plt.plot(x, h[0])
plt.plot(x, h[1])

[<matplotlib.lines.Line2D at 0x75451213ad50>]

Checks for numerical derivative

# recharge inside polygon (should be 0.01)
x = 20
y = 60
d = 0.01
d2hdx2 = (ml.head(x + d, y) - 2 * ml.head(x, y) + ml.head(x - d, y)) / (d**2)
d2hdy2 = (ml.head(x, y + d) - 2 * ml.head(x, y) + ml.head(x, y - d)) / (d**2)
d2hdx2 + d2hdy2
aqin = ml.aq.inhomlist[0]
print("recharge from numerical derivative: ", np.sum(aqin.T * (d2hdx2 + d2hdy2)))
h = ml.head(x, y)
print("leakage from aq0 to aq1 from head difference: ", (h[1] - h[0]) / aqin.c[1])
print(
    "leakage from aq0 to aq1 from num. derivative: ",
    aqin.T[1] * (d2hdx2[1] + d2hdy2[1]),
)

recharge from numerical derivative:  -0.009999998136223098
leakage from aq0 to aq1 from head difference:  -0.006153846153845954
leakage from aq0 to aq1 from num. derivative:  -0.006153845006906522