Test tidal response with analytic solutions#
This notebook shows some validation of tidal wave propagation in a ModelXsection against known formulas from literature (Bruggeman, 1999: Analytical solutions of geohydrological problems).
Three situations are shown:
Bruggeman 128.01: tidal fluctation of open water, in a confined aquifer with open boundary at x=0
Bruggeman 128.03: tidal fluctation of open water, in a leaky aquifer with open boundary at x=0
Bruggeman 128.04: tidal fluctation of open water, in a leaky aquifer with entry resistance at x=0
import matplotlib.pyplot as plt
import numpy as np
import timflow.transient as tft
Here we define some solutions from the book of Bruggeman.
(Note 1: Note how easily numpy deals with the complex algebra (splitting into an imaginary and a real part).
(Note 2: We might move the Bruggeman code to a new repository: https://github.com/dbrakenhoff/bruggeman).
def bruggeman_128_01(x, t, h, S, k, D, tau):
"""Tidal fluctuation open water, confined aquifer with open boundary (x = 0).
From Bruggeman 128.01
h = amplitude of tidal fluctuation, [m]
k = hydraulic conductivity [m/d]
D = aquifer thickness [m]
S = storage coefficient [-]
tau = tidal period [d]
"""
beta = np.sqrt(S / (k * D))
omega = 2 * np.pi / tau
omega_accent = beta * np.sqrt(omega / 2)
return h * np.exp(-omega_accent * x) * np.sin(omega * t - omega_accent * x)
def bruggeman_128_03(x, t, h, S, k, D, tau, c):
"""Tidal fluctuation open water, leaky aquifer with open boundary (x = 0).
From Bruggeman 128.03
h = amplitude of tidal fluctuation, [m]
k = hydraulic conductivity [m/d]
D = aquifer thickness [m]
S = storage coefficient [-]
tau = tidal period [d]
c = leakance [d]
"""
beta = np.sqrt(S / (k * D))
eta = 1 / (c * S)
omega = 2 * np.pi / tau
a = np.real(np.sqrt(eta + 1j * omega))
b = np.imag(np.sqrt(eta + 1j * omega))
return h * np.exp(-beta * a * x) * np.sin(omega * t - beta * b * x)
def bruggeman_128_04(x, t, h, S, k, D, tau, c, w):
"""Tidal fluctuation open water, leaky aquifer with entrance resistance (x = 0).
From Bruggeman 128.04
h = amplitude of tidal fluctuation, [m]
k = hydraulic conductivity [m/d]
D = aquifer thickness [m]
S = storage coefficient [-]
tau = tidal period [d]
c = leakance [d]
w = entry resistance at x=0 [d]
"""
beta = np.sqrt(S / (k * D))
eta = 1 / (c * S)
omega = 2 * np.pi / tau
theta = 1 / (np.power(beta, 2) * np.power(k, 2) * np.power(w, 2))
a = np.real(np.sqrt(eta + 1j * omega))
b = np.imag(np.sqrt(eta + 1j * omega))
return (
h
* np.sqrt(theta)
* np.exp(-beta * a * x)
* np.sin(omega * t - beta * b * x - np.arctan(b / (a + np.sqrt(theta))))
/ (np.sqrt(np.power((a + np.sqrt(theta)), 2) + np.power(b, 2)))
)
The analytic solution is for a river with varying head that has been varying for ever.
In timflow, head is simulated for several days to get the model to spin-up.
By using a sine function, the head starts at zero (as should be the case in timflow).
def head_river(h, t, tau, tp=0):
return h * np.sin(2 * np.pi * (t - tp) / tau)
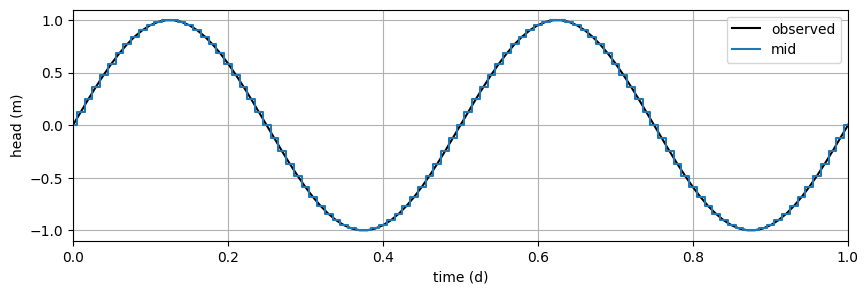
Below the sine (water level on river) is split into steps as shown in the example How to model a fluctuating head boundary. We use a small timestep (\(\Delta t\))
# Parameters of tidal wave
tau = 0.5 # tidal period, d
h_tidal = 1 # amplitude of tidal fluctuation, m
tmax = 5 # day
delt = 0.01 # day
t = np.arange(0, tmax, delt)
hexact = head_river(h_tidal, t, tau)
hmid = 0.5 * (
head_river(h_tidal, t - delt / 2, tau) + head_river(h_tidal, t + delt / 2, tau)
)
tmid = np.hstack((0, 0.5 * (t[:-1] + t[1:])))
# plot
plt.figure(figsize=(10, 3))
plt.plot(t, hexact, "k", label="observed")
plt.step(tmid, hmid, where="post", label="mid")
plt.xlim(0, 1)
plt.xlabel("time (d)")
plt.ylabel("head (m)")
plt.legend()
plt.grid()
Bruggeman 128.01 - Confined, no entry resistance#
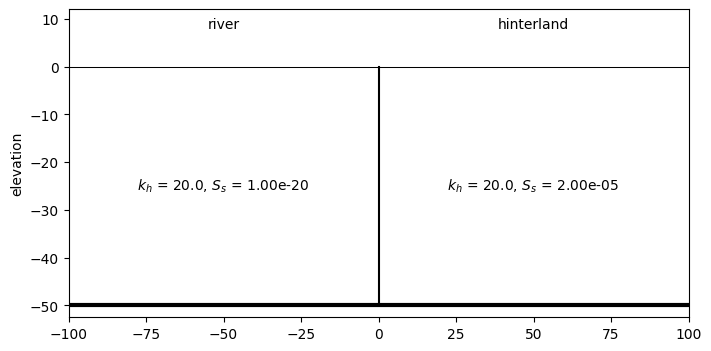
Create the timflow model for comparison with Bruggeman 128.01 (confined, no entry resistance).
In this example, we use the 1D inhomogeneities because of the nice plotting. The same result could be reached with a ‘normal’ timflow model.
In all the timflow models, the left-hand inhomogeneity (river) is shown for illustration purposes. That inhomogeneity is only created to satisfy the requirement of ModelXsection to have inhoms for \(-\infty<x<\infty\).
The hydraulic boundary river_hls is modeled as a River1D at x=0.
# parameters
k = 20.0 # hydraulic conductivity, m/d
H = 50.0 # thickness of aquifer, m
T = k * H # transmissivity, m^2/d
S = 0.001 # storage coefficient of aquifer, [-]
Saq = S / H # specific storage [1/m]
ml = tft.ModelXsection(naq=1, tmin=1e-4, tmax=1e2)
riv = tft.XsectionMaq(
model=ml,
x1=-np.inf,
x2=0,
kaq=k,
z=[0, -H],
Saq=1e-20,
Sll=1e-20,
topboundary="confined",
phreatictop=False,
name="river",
)
land = tft.XsectionMaq(
model=ml,
x1=0,
x2=np.inf,
kaq=k,
z=[0, -H],
Saq=Saq,
topboundary="confined",
phreatictop=False,
name="hinterland",
)
# Use a small offset to avoid a singular matrix.
small = 1e-5
river_hls = tft.River1D(
model=ml, xls=0 - small, tsandh=list(zip(tmid, hmid, strict=True))
)
ml.solve()
ax = riv.plot(params=True, names=True, labels=False)
land.plot(ax=ax, params=True, names=True, labels=False)
river_hls.plot(ax=ax)
ax.set_xlim(-100, 100)
ax.set_ylim(ymax=12);
self.neq 3
solution complete
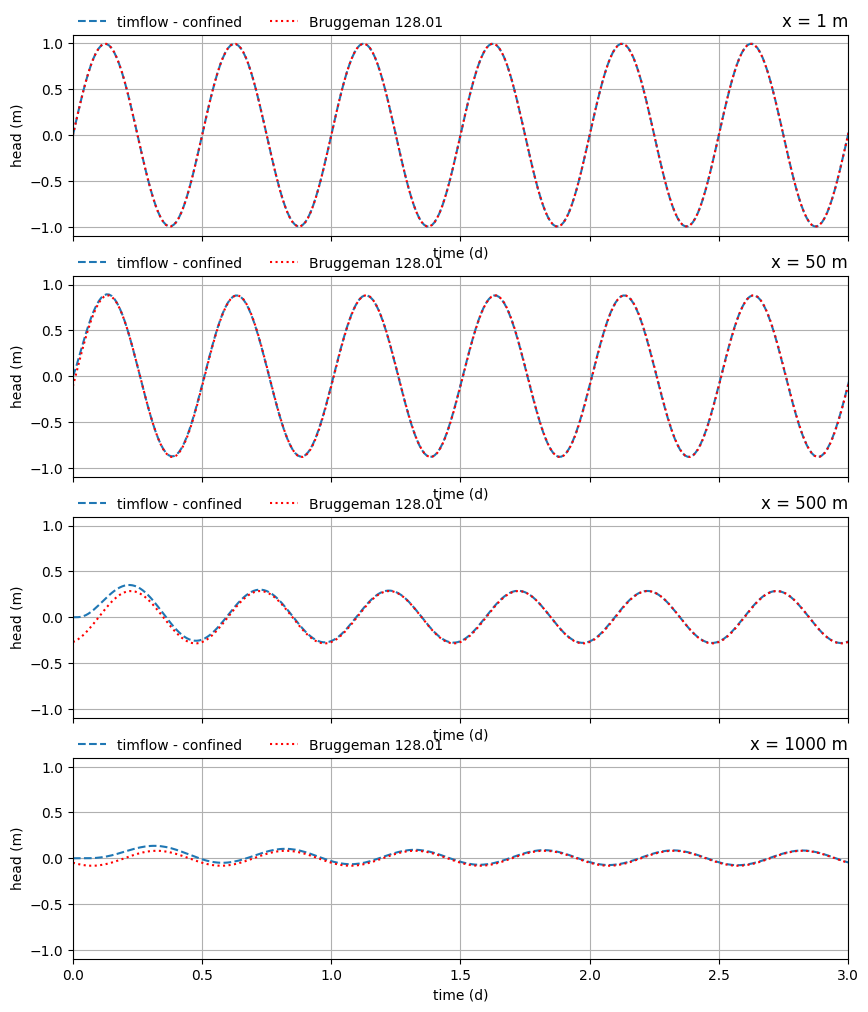
Let’s compare the head at several locations.
As can be seen from the lowest graph \(x = 500\), the timflow model needs some spinup time, but after a few days the graphs are similar.
xlocs = [1, 50, 500, 1000]
tp = t
f, axes = plt.subplots(
len(xlocs), 1, figsize=(10, 3 * len(xlocs)), sharex=True, sharey=True
)
for i in range(len(xlocs)):
h = ml.head(xlocs[i], 0, tp)
axes[i].plot(tp, h[0], label="timflow - confined", linestyle="--")
h_128_01 = bruggeman_128_01(xlocs[i], tp, h_tidal, S, k, H, tau)
axes[i].plot(tp, h_128_01, "r", label="Bruggeman 128.01", linestyle=":")
axes[i].set_title(f"x = {xlocs[i]} m", loc="right")
axes[i].legend(loc=(0, 1), frameon=False, ncol=2)
axes[i].grid()
axes[i].set_xlabel("time (d)")
axes[i].set_ylabel("head (m)")
axes[i].set_xlim([0, 3])
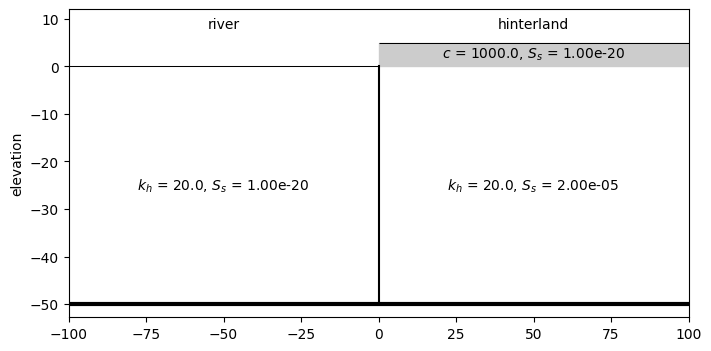
Bruggeman 128.03 Leaky, no entry resistance#
Create a timflow model for comparison with Bruggeman 128.03 (leaky, no entry resistance).
# Additional parameters for this model:
c = 1000 # leakage factor, d
# The model
ml2 = tft.ModelXsection(naq=1, tmin=1e-4, tmax=1e2)
riv2 = tft.XsectionMaq(
model=ml2,
x1=-np.inf,
x2=0,
kaq=k,
z=[0, -H],
Saq=1e-20,
Sll=1e-20,
topboundary="confined",
phreatictop=False,
name="river",
)
land2 = tft.XsectionMaq(
model=ml2,
x1=0,
x2=np.inf,
kaq=k,
z=[5, 0, -H],
c=c,
Saq=Saq,
topboundary="semi",
phreatictop=False,
name="hinterland",
)
# Use a small offset to avoid a singular matrix.
small = 1e-5
river_hls2 = tft.River1D(
model=ml2, xls=0 - small, tsandh=list(zip(tmid, hmid, strict=True))
)
ml2.solve()
ax = riv2.plot(params=True, names=True, labels=False)
land2.plot(ax=ax, params=True, names=True, labels=False)
river_hls2.plot(ax=ax)
ax.set_xlim(-100, 100)
ax.set_ylim(ymax=12);
self.neq 3
solution complete
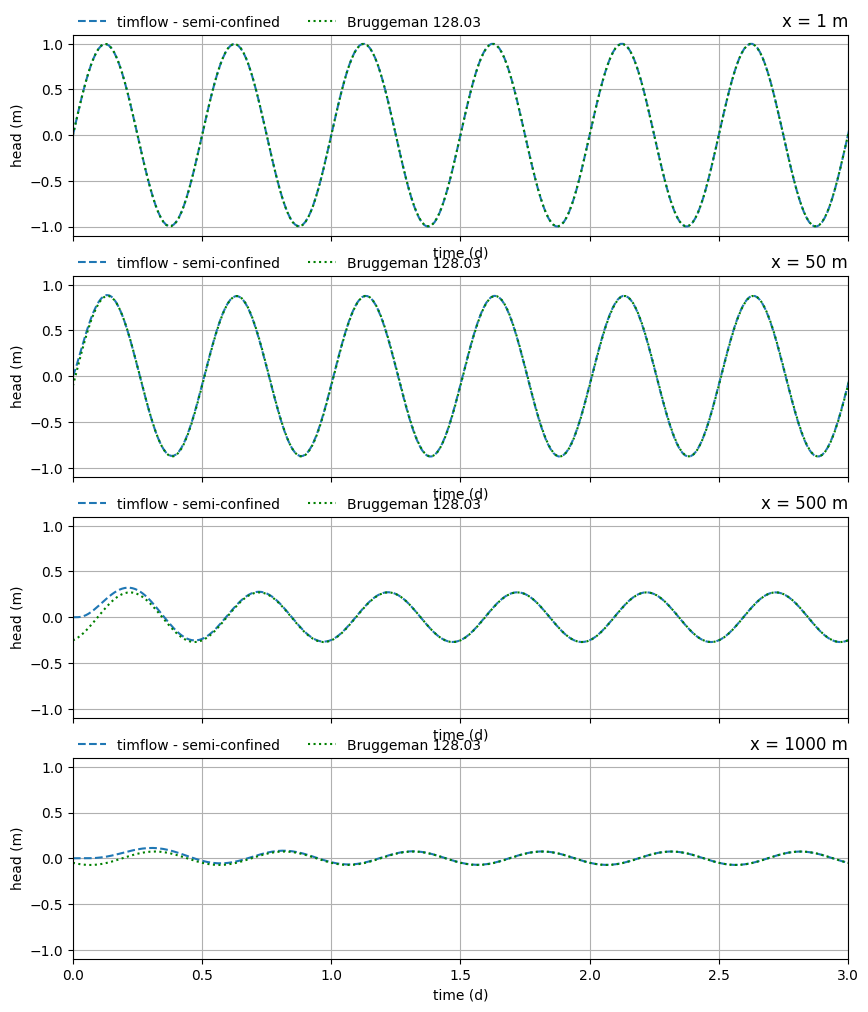
Again, compare heads at several locations.
xlocs = [1, 50, 500, 1000]
tp = t
f, axes = plt.subplots(
len(xlocs), 1, figsize=(10, 3 * len(xlocs)), sharex=True, sharey=True
)
for i in range(len(xlocs)):
h = ml2.head(xlocs[i], 0, tp)
axes[i].plot(tp, h[0], label="timflow - semi-confined", linestyle="--")
h_128_03 = bruggeman_128_03(xlocs[i], tp, h_tidal, S, k, H, tau, c)
axes[i].plot(tp, h_128_03, "g", label="Bruggeman 128.03", linestyle=":")
axes[i].set_title(f"x = {xlocs[i]} m", loc="right")
axes[i].legend(loc=(0, 1), frameon=False, ncol=2)
axes[i].grid()
axes[i].set_xlabel("time (d)")
axes[i].set_ylabel("head (m)")
axes[i].set_xlim([0, 3])
Bruggeman 128.04 Leaky, with entry resistance#
Create a timflow model for comparison with Bruggeman 128.04 (leaky, with entry
resistance at x=0).
The entry resistance is added to the River1D river_hls by adding the keyword argument res=w.
# Additional parameters for this model:
w = 20 # entry resistance at x=0, d
# The model
ml3 = tft.ModelXsection(naq=1, tmin=1e-4, tmax=1e2)
riv3 = tft.XsectionMaq(
model=ml3,
x1=-np.inf,
x2=0,
kaq=k,
z=[0, -H],
Saq=1e-20,
Sll=1e-20,
topboundary="confined",
phreatictop=False,
name="river",
)
land3 = tft.XsectionMaq(
model=ml3,
x1=0,
x2=np.inf,
kaq=k,
z=[5, 0, -H],
c=c,
Saq=Saq,
topboundary="semi",
phreatictop=False,
name="hinterland",
)
# Use a small offset to avoid a singular matrix.
small = 1e-5
river_hls3 = tft.River1D(
model=ml3,
xls=0 - small,
tsandh=list(zip(tmid, hmid, strict=True)),
res=w,
)
ml3.solve()
ax = riv3.plot(params=True, names=True, labels=False)
land3.plot(ax=ax, params=True, names=True, labels=False)
river_hls3.plot(ax=ax)
ax.set_xlim(-100, 100)
ax.set_ylim(ymax=12)
self.neq 3
solution complete
(-52.75, 12.0)

xlocs = [1, 50, 500, 1000]
tp = t
f, axes = plt.subplots(
len(xlocs), 1, figsize=(10, 3 * len(xlocs)), sharex=True, sharey=True
)
for i in range(len(xlocs)):
h = ml3.head(xlocs[i], 0, tp)
axes[i].plot(tp, h[0], label="timflow - leaky + entry resistance", linestyle="--")
h_128_04 = bruggeman_128_04(xlocs[i], tp, h_tidal, S, k, H, tau, c, w)
axes[i].plot(tp, h_128_04, "k", label="Bruggeman 128.04", linestyle=":")
axes[i].set_title(f"x = {xlocs[i]} m", loc="right")
axes[i].legend(loc=(0, 1), frameon=False, ncol=2)
axes[i].grid()
axes[i].set_xlabel("time (d)")
axes[i].set_ylabel("head (m)")
axes[i].set_xlim([0, 3])
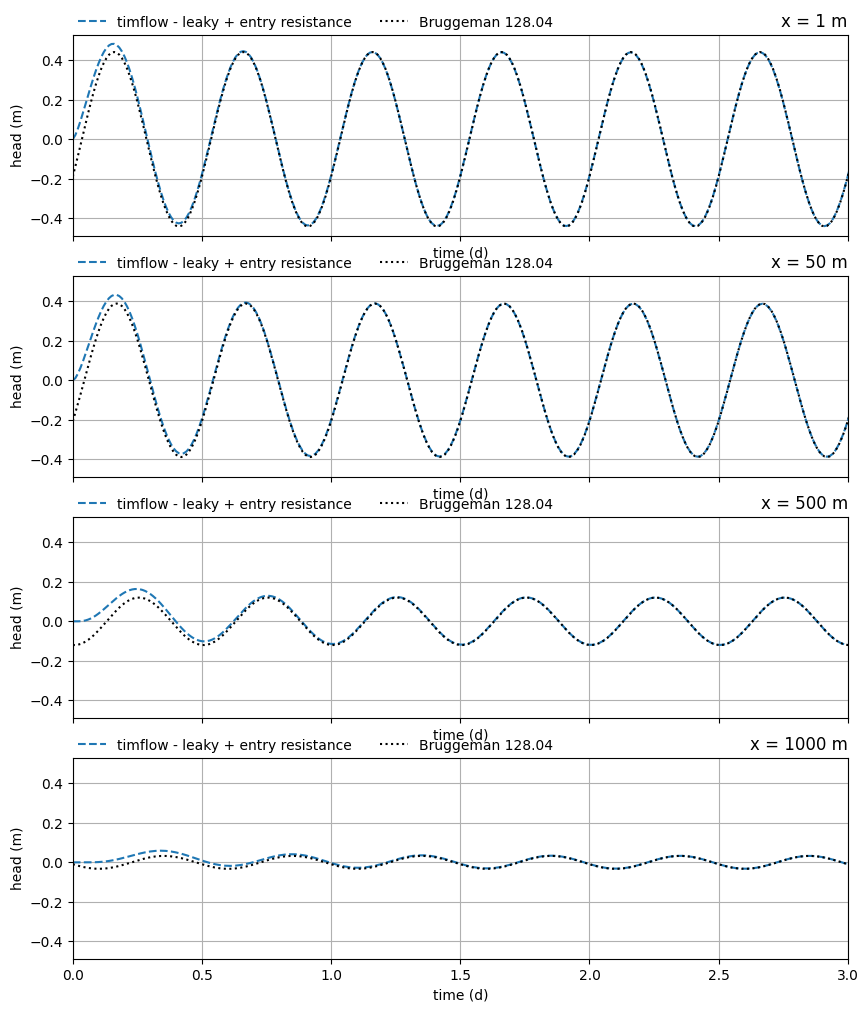
As can be seen, all three cases are replicated accurately after approximately 2 days spinup time.
In the case with entry resistance, the head in the aquifer is already considerably damped compared to the open water fluctuation, even at a small distance (x=1 m).
